G -- Mechanics of the Pursuit Curve
Lambda
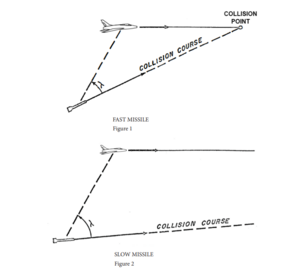
Lambda limit is simply the max look-angle between the axis of the gyro-seeker and the longitudinal axis of the missile – a 25-degree cone with its center along the longitudinal axis of the missile. Why are we interested in this lambda limitation? It is possible for a pilot to satisfy the conditions of IR, range, and G, yet be outside the lambda capability of the missile. Lambda limit may be exceeded by a combination of two factors: low missile velocity and high angle-off.
(1) Low Missile Velocity: One-half second after launch, Sidewinder turns to establish a collision course with the target. Two seconds after launch, it has a velocity 1.7 Mach greater than that of the launch aircraft. To establish a collision course, Sidewinder turns 3 1 ∕ 2 times the rate of the gyro-seeker axis to reduce the line of sight rate to zero, or establish a constant angular relationship between the missile and the target. After rocket motor burn-out, the missile begins to slow down. In order to maintain a collision course after deceleration, the gyro-seeker must look farther and farther to the side as it nears the target. In other words, as illustrated by figures 1 and 2, as the missile slows down, the lambda angle increases until collision occurs.
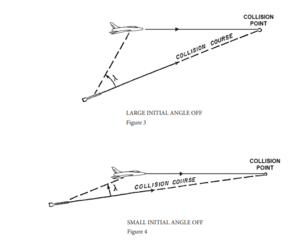
(2) High Angle-Off, the other basic cause of lambda-limiting is understood by considering a missile which, immediately upon launching, could turn onto the collision course. The line-of-sight angle would remain constant and the gyro-seeker would thus remain with its axis along the initial pursuit heading. It can be seen in figures 3 and 4 that the collision course for launching well off the tail differs in direction from the initial heading much more than does the collision course for launching slightly off the tail.
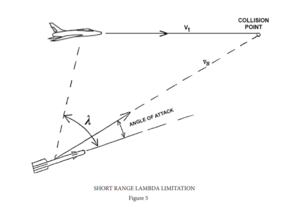
Consequently, the higher the angle-off, the greater the lambda angle. At long range (within max missile range) lambda limitation occurs at smaller angles-off, because of the effect of lambda-limitation on decreasing missile velocity. At short range, lambda limitation is caused by the sharp turn which the missile must perform. You will recall that if an attacker fires with any appreciable angle-off at short range, he will be very near his 2G limitation, or near the 10G limitation of the missile itself. This means that the missile is turning sharply to set up its collision course. The sharper the turn, the higher the missile angle of attack. As shown in figure 5, the angle of attack adds to the lambda angle so that lambda limit is reached. When lambda limit is exceeded, the gyro-seeker bumps against a mechanical stop, slows the gyro to a halt and the missile goes ballistic. Since we have no instrumentation available to measure lambda limit, we provide an artificial means to represent this lambda limitation – do not fire at angles-off greater than 30°. At 40,000 feet and above, do not exceed 10° angle-off – this is primarily because of servo-bias (poor burning of powder). This will preclude the possibility of an attacking pilot exceeding the lambda limitation of his missile.
In order to kill with Sidewinder, you must be within the firing envelope as defined by the infrared, range, G and lambda limitations. If a pilot exceeds any one of these limits, kill-probability drops drastically. For practical purposes, we can define the missile firing envelope as a 60° cone emanating from the tail of the target aircraft, with its length dependent upon altitude and rate of closure (Delta Mach). For future use, we will describe this cone as an angular velocity cone or a cone of maximum performance.
G -- Mechanics of the Pursuit Curve