The Overhead Attack
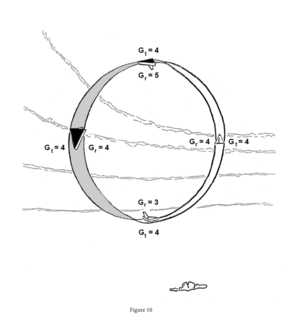
The overhead attack, as compared to the high-side or level attack, has the apparent advantage of maintaining airspeed and G because the thrust vector and gravity act together to provide a greater total force. However, to determine whether or not there is a real advantage, let’s examine the difference between rate of turn (GR) and total G. To digress, let’s assume that an aircraft is in straight-and-level flight. How many G will show on the G-meter? One G. Now, let’s assume that an aircraft is in straight-andlevel flight, but upside down. How many G will show on the G-meter? One negative G. Now remembering these relationships, let’s note the total and radial G relationships at four points around a loop – the pull-up, the 90° point, the 180° point, and the 270° point. For example: let’s assume that the aircraft is pulling 4 total G at the pull up as illustrated in figure 10. How many radial G is it pulling? Three. Then, in effect, we have added 3 G to the 1G needed for straight-and-level flight, to give us 4 total G at pull-up. At the 90° point,when pulling 4 total G, we will also be pulling 4 radial G. At this point, gravity is 90° from our vertical axis, thereby exerting no pull along this axis — instead, it is a drag factor action 180° from the aircraft line of flight. At the 180° point, when we are pulling 4 total G, we will have 5 radial G, thereby giving us a turn rate – at a given airspeed – greater than at any other point on the loop. In other words, as compared to the pull-up, gravity (1G) acts in the opposite direction, therefore gravity must add to, rather than subtract from total G, to provide a greater radial G. At the 270° point, once again, total G equals radial G except that gravity acts in the same direction as the aircraft line of flight. From the 270° point on, radial G diminishes in relation to total G until the pull-up point is reached. At this point we again have 1G difference between total and radial G.
In an overhead attack, to determine the difference between total and radial G, we may use the following formula:
Gt = Gr + Cosθ
Where
Gt = Total G
Gr = Radial G
Cosθ = Cosine of the angle off
It is obvious, from the formula, that the relationship between total and radial G is considerably different from that experienced in a high-side pass. Example:
In a Level Pass where Gt = 4,
Gr = √(16 - 1) = 3.87
In an Overhead Pass at 30° angle-off where Gt = 4
Gr = Gt - Cosθ or Gr = 4 - 0.866 = 3.14
As shown in the example above, if an attacker is force to fire inside an opponent’s maximum performance cone – at angles of less than 30° – this means that from .866 to 1 more G, above radial G, is necessary to track a given target. Thus, as compared to a high-side attack, even though an attacker may have an apparent advantage in maintaining higher G, it is largely wiped out by the greater difference between radial and total G. The important thing to keep in mind here is that the overhead attack offers no significant advantages over the high-side attack.