Cartesian product

"Cartesian square" redirects here. For Cartesian squares in category theory, see Cartesian square (category theory).

Cartesian product $\scriptstyle A\times B$ of the sets $\scriptstyle A=\{x,y,z\}$ and $\scriptstyle B=\{1,2,3\}$

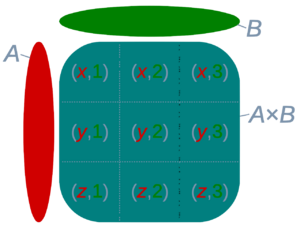
In mathematics, specifically set theory, the Cartesian product of two sets A and B, denoted A × B, is the set of all ordered pairs (a, b) where a is in A and b is in B. In terms of set-builder notation, that is

$A\times B=\{(a,b)\mid a\in A\ {\mbox{ and }}\ b\in B\}.$

A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product rows × columns is taken, the cells of the table contain ordered pairs of the form (row value, column value).

One can similarly define the Cartesian product of n sets, also known as an n-fold Cartesian product, which can be represented by an n-dimensional array, where each element is an n-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets.

The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product.