In aerodynamics, the flight envelope, service envelope, or performance envelope of an aircraft or spacecraft refers to the capabilities of a design in terms of airspeed and load factor or atmospheric density, often simplified to altitude.[1][2] The term is somewhat loosely applied, and can also refer to other measurements such as maneuverability. When a plane is pushed, for instance by diving it at high speeds, it is said to be flown "outside the envelope", something considered rather dangerous.
Flight envelope is one of a number of related terms that are all used in a similar fashion. It is perhaps the most common term because it is the oldest, first being used in the early days of test flying. It is closely related to more modern terms known as extra power and a doghouse plot which are different ways of describing a flight envelope. In addition, the term has been widened in scope outside the field of engineering, to refer to the strict limits in which an event will take place or more generally to the predictable behavior of a given phenomenon or situation, and hence, its "flight envelope".
Extra power
Extra power, or specific excess power,[3] is a very basic method of determining an aircraft's flight envelope. It is easily calculated, but as a downside does not tell very much about the actual performance of the aircraft at different altitudes.
Choosing any particular set of parameters will generate the needed power for a particular aircraft for those conditions. For instance a Cessna 150 at 2,500-foot (760 m) altitude and 90-mile-per-hour (140 km/h) speed needs about 60 horsepower (45 kW) to fly straight and level. The C150 is normally equipped with a 100-horsepower (75 kW) engine, so in this particular case the plane has 40 horsepower (30 kW) of extra power. In overall terms this is very little extra power, 60% of the engine's output is already used up just keeping the plane in the air. The leftover 40 hp is all that the aircraft has to maneuver with, meaning it can climb, turn, or speed up only a small amount. To put this in perspective, the C150 could not maintain a 2g (20 m/s²) turn, which would require a minimum of 120 horsepower (89 kW) under the same conditions.
For the same conditions a fighter aircraft might require considerably more power due to their wings being designed for high speed, high agility, or both. It could require 10,000 horsepower (7.5 MW) to achieve similar performance. However modern jet engines can provide considerable power with the equivalent of 50,000 horsepower (37 MW) not being atypical. With this amount of extra power the aircraft can achieve very high maximum rate of climb, even climb straight up, make powerful continual maneuvers, or fly at very high speeds.
Doghouse plot
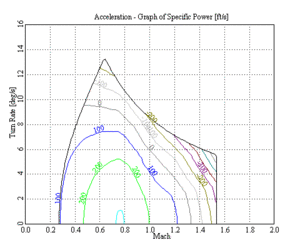
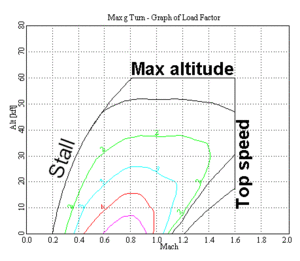
A doghouse plot generally shows the relation between speed at level flight and altitude, although other variables are also possible. It takes more effort to make than an extra power calculation, but in turn provides much more information such as ideal flight altitude. The plot typically looks something like an upside-down U and is commonly referred to as a doghouse plot due to its resemblance to a kennel (sometimes known as a 'doghouse' in American English). The diagram on the right shows a very simplified plot which shall be used to explain the general shape of the plot.
The outer edges of the diagram, the envelope, show the possible conditions that the aircraft can reach in straight and level flight. For instance, the aircraft described by the black altitude envelope on the right can fly at altitudes up to about 52,000 feet (16,000 m), at which point the thinner air means it can no longer climb. The aircraft can also fly at up to Mach 1.1 at sea level, but no faster. This outer surface of the curve represents the zero-extra-power condition. All of the area under the curve represents conditions that the plane can fly at with power to spare, for instance, this aircraft can fly at Mach 0.5 at 30,000 feet (9,100 m) while using less than full power.
In the case of high-performance aircraft, including fighters, this "1-g" line showing straight-and-level flight is augmented with additional lines showing the maximum performance at various g loadings. In the diagram at right, the green line represents, 2-g, the blue line 3-g, and so on. The F-16 Fighting Falcon has a very small area just below Mach 1 and close to sea level where it can maintain a 9-g turn.
Flying outside the envelope is possible, since it represents the straight-and-level condition only. For instance diving the aircraft allows higher speeds, using gravity as a source of additional power. Likewise higher altitude can be reached by first speeding up and then going ballistic, a maneuver known as a zoom climb.
Stalling speed
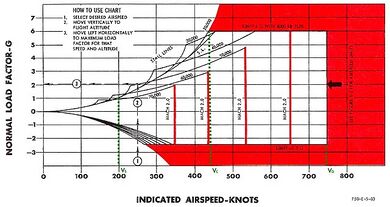
All fixed-wing aircraft have a minimum speed at which they can maintain level flight, the stall speed (left limit line in the diagram). As the aircraft gains altitude the stall speed increases; since the wing is not growing any larger the only way to support the aircraft's weight with less air is to increase speed. While the exact numbers will vary widely from aircraft to aircraft, the nature of this relationship is typically the same; plotted on a graph of speed (x-axis) vs. altitude (y-axis) it forms a diagonal line.
Service ceiling
Inefficiencies in the wings also make this line "tilt over" with increased altitude, until it becomes horizontal and additional speed will not result in increased altitude. This maximum altitude is known as the service ceiling (top limit line in the diagram), and is often quoted for aircraft performance. The area where the altitude for a given speed can no longer be increased at level flight is known as zero rate of climb and is caused by the lift of the aircraft getting smaller at higher altitudes, until it no longer exceeds gravity.
Top speed
The right side of the graph represents the maximum speed of the aircraft. This is typically sloped in the same manner as the stall line due to air resistance getting lower at higher altitudes, up to the point where an increase in altitude no longer increases the maximum speed due to lack of oxygen to feed the engines.
The power needed varies almost linearly with altitude, but the nature of drag means that it varies with the square of speed—in other words it is typically easier to go higher than faster, up to the altitude where lack of oxygen for the engines starts to play a significant role.
Velocity vs. load factor chart
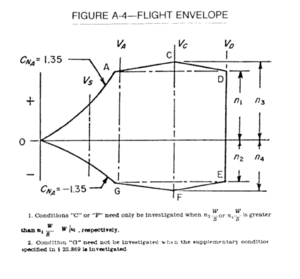
A chart of velocity versus load factor (or V-n diagram) is another way of showing limits of aircraft performance. It shows how much load factor can be safely achieved at different airspeeds.[3]
At higher temperatures, air is less dense and planes must fly faster to generate the same amount of lift. High heat may reduce the amount of cargo a plane can carry, increase the length of runway a plane needs to take off, and make it more difficult to avoid obstacles such as mountains. In unusual weather conditions this may make it unsafe or uneconomical to fly, occasionally resulting in the cancellation of commercial flights.[4][5]
Side Notes
Although it is easy to compare aircraft on simple numbers such as maximum speed or service ceiling, an examination of the flight envelope will reveal far more information. Generally a design with a larger area under the curve will have better all-around performance. This is because when the plane is not flying at the edges of the envelope, its extra power will be greater, and that means more power for things like climbing or maneuvering. General aviation aircraft have very small flight envelopes, with speeds ranging from perhaps 50 to 200 mph, whereas the extra power available to modern fighter aircraft result in huge flight envelopes with many times the area. As a trade-off however, military aircraft often have a higher stalling speed. As a result of this the landing speed is also higher.
"Pushing the envelope"
This phrase is used to refer to an aircraft being taken to or beyond its designated altitude and speed limits.[6] By extension, this phrase may be used to mean testing other limits, either within aerospace or in other fields e.g. Plus ultra (motto).[7]
See also
Notes
- ↑ §23.333 Flight envelope Archived 2012-04-02 at the Wayback Machine
- ↑ Flight envelope – diagram Archived June 1, 2010, at the Wayback Machine
- ↑ 3.0 3.1 Sinclair, Edward J. "The Army Aviator's Handbook for Manoeuvring Flight and Power Management" Archived 2011-07-17 at the Wayback Machine. p. 25. United States Army Aviation Branch, 24 March 2005. Accessed: 6 January 2011.
- ↑ Why planes can’t fly when it’s too hot, and other ways our civilization can’t take the heat
- ↑ Why Planes Can't Fly In Extreme Heat
- ↑ Quinion, Michael. Push the envelope World Wide Words. Accessed: 6 January 2011.
- ↑ G.W. Poulos & Daniel Lindley. "What Is a Flight Envelope?" WiseGeek, 6 May 2014. Accessed: 16 May 2014.