Portal maintenance status: (October 2020)
|
{{{title}}}
| Complex systems approach |
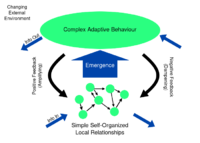
Systems science is an transdisciplinary[1] field that studies the nature of systems—from simple to complex—in nature, society, cognition, engineering, technology and science itself. To systems scientists, the world can be understood as a system of systems. The field aims to develop interdisciplinary foundations that are applicable in a variety of areas, such as psychology, biology, medicine, communication, business management, engineering, and social sciences.
Systems science covers formal sciences such as complex systems, cybernetics, dynamical systems theory, information theory, linguistics or systems theory. It has applications in the field of the natural and social sciences and engineering, such as control theory, operations research, social systems theory, systems biology, system dynamics, human factors, systems ecology, systems engineering and systems psychology. Themes commonly stressed in system science are (a) holistic view, (b) interaction between a system and its embedding environment, and (c) complex (often subtle) trajectories of dynamic behavior that sometimes are stable (and thus reinforcing), while at various 'boundary conditions' can become wildly unstable (and thus destructive). Concerns about Earth-scale biosphere/geosphere dynamics is an example of the nature of problems to which systems science seeks to contribute meaningful insights.
{{{title}}}
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a tornado in Brazil.
Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as: (Full article...)Selected picture
The page "Portal:Systems science/Picture/5" does not exist.
{{{title}}}
{{{title}}}
{{{title}}}
Lua error in Module:Transclude_DYK at line 13: No content for page Portal:Systems science/Did you know.
{{{title}}}
<categorytree depth="1">Systems science</categorytree>
{{{title}}}
Lua error: bad argument #2 to 'title.new' (unrecognized namespace name 'Portal').
{{{title}}}
{{{title}}}
|
File:Nuvola apps korganizer.svg |
Here are some tasks awaiting attention:
|