True anomaly

The true anomaly of point P is the angle f. The center of the ellipse is point C, and the focus is point F.

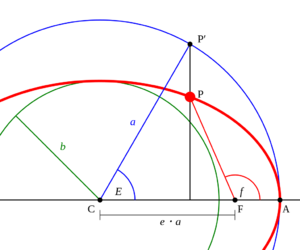
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits).

The true anomaly is usually denoted by the Greek letters $ν$ or $θ$ , or the Latin letter $f$ , and is usually restricted to the range 0–360° (0–2π^c).

The true anomaly $f$ is one of three angular parameters (anomalies) that defines a position along an orbit, the other two being the eccentric anomaly and the mean anomaly.

Formulas

From state vectors

For elliptic orbits, the true anomaly $ν$ can be calculated from orbital state vectors as:

\nu =\arccos \left({\frac {e\cdot r}{|e|\cdot |r|}}\right)

(if r ⋅ v < 0 then replace ν by 2π − ν)

(if r ⋅ v < 0 then replace

ν

by 2

π

−

ν

)

where:

v is the orbital velocity vector of the orbiting body,
e is the eccentricity vector,
r is the orbital position vector (segment FP in the figure) of the orbiting body.

Circular orbit

For circular orbits the true anomaly is undefined, because circular orbits do not have a uniquely determined periapsis. Instead the argument of latitude u is used:

u=\arccos {{\mathbf {n} \cdot \mathbf {r} } \over {\mathbf {\left|n\right|} \mathbf {\left|r\right|} }}

(if r_z < 0 then replace u by 2

π

− u)

where:

n is a vector pointing towards the ascending node (i.e. the z-component of n is zero).
r_z is the z-component of the orbital position vector r

Circular orbit with zero inclination

For circular orbits with zero inclination the argument of latitude is also undefined, because there is no uniquely determined line of nodes. One uses the true longitude instead:

l=\arccos {r_{x} \over {\mathbf {\left|r\right|} }}

(if v_x > 0 then replace

l

by 2

π

−

l

)

where:

r_x is the x-component of the orbital position vector r
v_x is the x-component of the orbital velocity vector v.

From the eccentric anomaly

The relation between the true anomaly $ν$ and the eccentric anomaly $E$ is:

\cos {\nu }={{\cos {E}-e} \over {1-e\cos {E}}}

or using the sine^[1] and tangent:

{\begin{aligned}\sin {\nu }&=<nowiki>{{{\sqrt {1-e^{2}\,}}\sin {E}}</nowiki> \over {1-e\cos {E}}}\\[4pt]<nowiki></nowiki>\tan {\nu }=<nowiki>{{\sin {\nu }}</nowiki> \over {\cos {\nu }}}&=<nowiki>{{{\sqrt {1-e^{2}\,}}\sin {E}}</nowiki> \over {\cos {E}-e}}\end{aligned}}

or equivalently:

\tan {\nu  \over 2}={\sqrt {{1+e\,} \over {1-e\,}}}\tan {E \over 2}

so

\nu =2\,\operatorname {arctan} \left(\,{\sqrt {{1+e\,} \over {1-e\,}}}\tan {E \over 2}\,\right)

Alternatively, a form of this equation was derived by ^[2] that avoids numerical issues when the arguments are near $\pm \pi$ , as the two tangents become infinite. Additionally, since ${\frac {E}{2}}$ and ${\frac {\nu }{2}}$ are always in the same quadrant, there will not be any sign problems.