Lambda -- Limitations of Our Weapons System in a Pursuit Curve Attack
Mechanics of the Pursuit Curve
To fully comprehend the limitations of our weapons system, so that we may develop effective tactics, we need to know something of the nature of the attack in which we will be employing Sidewinder – the pursuit curve attack. A pursuit curve attack is basically an attack in which the flight path of the attacking fighter is continuously pointed at a moving target. To provide an insight into this type of attack, we will employ the following formula:
W = Vf x Vt x Sinθ / 32.2N
Where
S = Range
Vf = Fighter velocity in feet per second
Vt = Target velocity in feet per second
Sinθ = Sine of the angle-off of the attacking fighter
N = Number of radial Gs pulled by the attacker
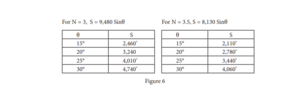
With the above formula, we can compute the range for a given G and angle-off for any combination of target and fighter speeds. It should be noted however, that the formula does not consider lead for target motion, nor does it represent the flight path of the attacking aircraft. Instead it represents distance/bearing relationships for a given set of values at a specific point in space. Despite the above limitations , the formula is still valid, in that it provides an insight into the problems associated with the pursuit curve. Study of the formula reveals: 1. The area of vulnerability is a narrow cone emanating from the tail of the target aircraft. This can be amply illustrated in the formula above by analyzing figure 6.
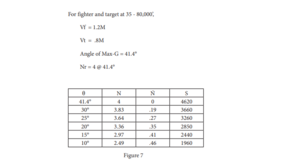
For fighter and target at 35,000’,
Vf = 1.2M = 693 KTAS = 1,170’ ∕ second
Vt = .8M = 463 KTAS = 782’ ∕ second
S = (Vf x Vt x Sinθ / 32.2N) = (28,450 x Sinθ / N)
As shown in figure 6, the cone becomes narrower at firing ranges if the fighter velocity and/or target velocity is increased. In other words, the attacking fighter will be forced to fire at smaller angles-off if he does not wish to increase his firing range. Reducing angle-off against bomber-type targets places the attacking fighter in the bomber’s effective cone of fire. Therefore, if the velocities of the target and fighter increase, and we do not reduce angle-off, the range must, of necessity, increase. The increase in range will be in proportion to the velocity increase of the fighter or the target. If both target and fighter velocities are increased, the increase in range will be a multiple of the increases of the fighter and target velocities (for example – if Vf and Vt are doubled, the range will be quadrupled).
2. The cone becomes narrower with an increase in altitude (the formula is a function of fighter velocity, G, and angle-off). It is a recognized fact that the available G of the fighter decreases with an increase in altitude and, as shown in the formula, any such decrease in G will be accompanied by an increase in range.
In a curve of pursuit, the rate of turn necessary to track a given target is determined by range, angle-off and target velocity. This rate of turn may be expressed by the following formula:
W = Vt x Sinθ / Range
Where
W = Radians per second
Vt = Target velocity in feet per second
Sinθ = Sine of the angle-off
On the basis of the formula, if angle-off diminishes more rapidly than the range, the rate of turn will decrease (this will occur in some part of the pursuit curve when the fighter velocity is less than twice the velocity of the target). If range diminishes more rapidly than angle-off, throughout the curve, the rate of turn or G will increase (this will occur when the fighter velocity is more than twice as great as the velocity of the target). To find the parts of the curve where we will achieve these increases or decreases in rates of turn, we can use the following formula:
CoSin of the angle-off where maximum G occurs = Vf / 2 x Vt
Where
Vf = Fighter velocity
Vt = Target velocity
NOTE: These two velocities may be expressed in knots, miles per hour, feet per second, or any other appropriate unit, as long as Vf and Vt are expressed in like values.
This formula will enable us to determine the point on the pursuit curve where maximum G will be encountered. For example: If we have a fighter with a velocity of 1.2 Mach attacking a target with a velocity of .8 Mach, the point of max-G will be about 41.4° angle-off. Therefore, in effect, we are saying that at angles greater than 41.4°, the rate of turn (or G) is increasing. At angles of less than 41.4° the rate of turn is decreasing. To further illustrate – if we have a fighter traveling at twice or greater than twice the speed of the target, the max-G point will occur at zero-degrees angle-off. In other words, there will be a G build-up or an increase in the rate of turn throughout the entire pass.
In pursuit attacks with today’s fighter-bomber velocities, a fighter is forced to fire under conditions where its velocity is less than twice that of the target. In this type of attack, the fighter is not only forced to fire at longer ranges, but also to fire where his rate of turn is decreasing. We can see from studying figure 7 that the attacker’s rate of turn is not only decreasing, but it is decreasing at an increasing rate. In other words, the attacker is being “sucked” or forced in-trail. As illustrated in figure 7, the attacker loses .19 G/sec at 30° angle-off. At 25° angle-off he loses .27 G ∕ sec and so on until at 10° angle-off he loses .45 G ∕ sec.
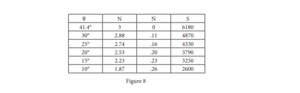
If the attacker decreases his G at the max-G point (with the same fighter velocities as shown is figure 8, he will be able to diminish his rate of G bleed-off. However, this will force him to fire at longer ranges. Naturally an attacker does not want to do this, because, as range increases, his bullet density decreases by a function of the square (if range doubles, bullet density quarters). As a result, an attacker must fire over a longer time span to deliver a lethal burst. At the same time, he must track a target smaller in perspective. Under these conditions, it becomes quite difficult to deliver an effective burst.
For fighter and target at 35 - 80,000’,
Vf = 1.2 Mach
Vt = 0.9 Mach
Angle of Max-G = 41.4°
Nr = 3 @ 41.4°
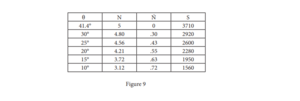
If the attacker increases his G at the Max-G point, as shown in figure 9, he will be able to fire at shorter ranges. However, if he does this, his G bleed-off will become even more rapid than originally shown.
For fighter and target at 35 - 80,000’,
Vf = 1.2 Mach
Vt = 0.8 Mach
Angle of Max-G = 41.4°
Nr = 5 @ 41.4°
N = Rate of Change G / sec²
Lambda -- Limitations of Our Weapons System in a Pursuit Curve Attack